栈和队列

栈

栈是限定在表的一端进行插入和删除运算的线性表，插入、删除的一端称为栈顶，另一端称为栈底。如果一个栈不含任何元素则称为空栈。 栈又称为后进先出线性表，简称为LIFO表。

比如装箱子，都是从底部开始一层一层往上放（入栈）；假如这时要拿底部那层的物品，是不是就需要从顶层开始一层一层拿出来（出栈）。

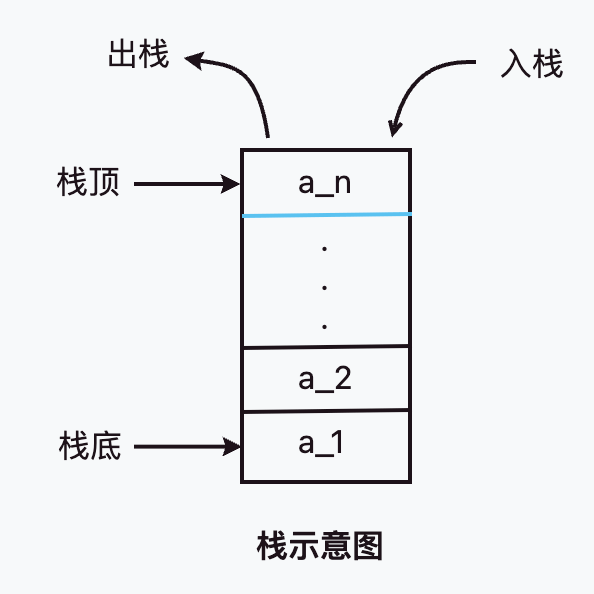
当栈满时，再进行入栈操作会产生“上溢”；当栈空时再进行出栈操作会产生“下溢”。

栈的基本运算有：

1. 置空栈
2. 判断栈空
3. 判断栈满
4. 入栈
5. 出栈
6. 取栈顶元素

📝 现在就在下面简单实现一下这些运算~

栈的定义

💡 JavaScript 中实现栈就非常简单了，通常使用数组模拟实现。

c

#define StackSize 100
typedef char DataType; // DataType 类型根据实际情况定，这里是 char
typedef struct {
	DataType data[StackSize];
	int top;
} SeqStack;
SeqStack s;

typescript

type SeqStack = string[]
const StackSize = 100 // 栈的长度，后面用到
const seqStack: SeqStack = [] // 注意 js 中数组长度是可变的，因此需要在入栈限制，后续讲到
// int top = seqStack.length - 1 // 因为数组长度就是栈顶的索引，因此没必要保存

// 还有一种方法，但不推荐
const seqStack: SeqStack = new Array(StackSize)
int top = -1 // 此时就需要记录栈顶索引了，数组长度不再表示栈顶索引。
// 注意：同时下面的出入栈也不能这么写了。

置空栈

c

void InitStack(SeqStack *S)
{
	// 原因数组的下标从0开始，因此不能使用0
  S->top = -1;
}

typescript

function initStack(s: SeqStack) {
	// 因为 JS 中数组在函数参数中传递的是引用，因此会修改到原数组变量
  s = []
}

判断栈空

c

int StackEmpty(SeqStack *S)
{
  return S->top == -1;
}

typescript

function stackEmpty(s: SeqStack) {
  return !!s.length
}

判断栈满

c

int StackFull(SeqStack *S)
{
  return S->top = StackSize - 1;
}

typescript

function stackFull(s: SeqStack) {
  return s.length === StackSize
}

入栈

JavaScript 中的出入栈就非常简单了，就是数组的 push、pop 方法。

c

void Push(SeqStack *S, DataType x)
{
  if (StackFull(S))
  {
    prinf('stack overflow');
  }
  else
  {
    S->top = S->top + 1;
    S->data[S->Top] = x;
  }
}

typescript

function push(s: SeqStack, x: string) {
  if(stackFull(s)) {
    console.error('stack overflow')
  } else {
    s.push(x)
  }
}

出栈

c

DataType Pop(SeqStack *S)
{
  if (StackEmpty(S))
  {
    prinf('stack underflow');
    exit(0);
  }
  else
  {
    return S->data[S->top--];
  }
}

typescript

function pop(s: SeqStack) {
  if (stackEmpty(s)) {
    throw new Error('stack underflow')
  } else {
    return s.pop()
  }
}function push(s: SeqStack, x: string) {
  if (stackFull(s)) {
    console.error('stack overflow')
  } else {
    s.push(x)
  }
}

取栈顶元素

c

DataType GetTop(SeqStack *S)
{
  if (StackEmpty(S))
  {
    prinf('stack underflow');
    exit(0);
  }
  else
  {
    return S->data[S->top];
  }
}

typescript

function getTop(s: SeqStack) {
  if (stackEmpty(s)) {
    throw new Error('stack underflow')
  } else {
    return s[s.length - 1]
  }
}

❗ 因为在某一些语言中，在声明数组时就需要确定分配的空间，为了克服固定空间所产生的溢出问题和空间浪费问题，还有一种栈的实现方式，使用链式存储结构来存储栈，称为链栈。 因为 JavaScript 中数组是可动态改变的，因此在大多数情况下都是使用它来实现，所以这里就不解释链栈了。 链式存储结构知识可以查看 👉🏻 《线性表》

应用场景（列举部分）

1. 括号匹配。
2. 回文数（比如 LeeCode 第9题）。
3. 递归实现原理。

队列

队列也是一种线性表，它只允许在表的一端进行元素插入，在另一端进行元素删除。允许插入（入队）的一端称为队尾，允许删除（出队）的一端称为队头。 队列称为先进先出表，简称FIFO表。

*比如排队上公交，排在最前的一端先上公交，后到的人只能到队尾进行排队等候。温馨提示文明出行，禁止插队。*🚌 🚌 🚌

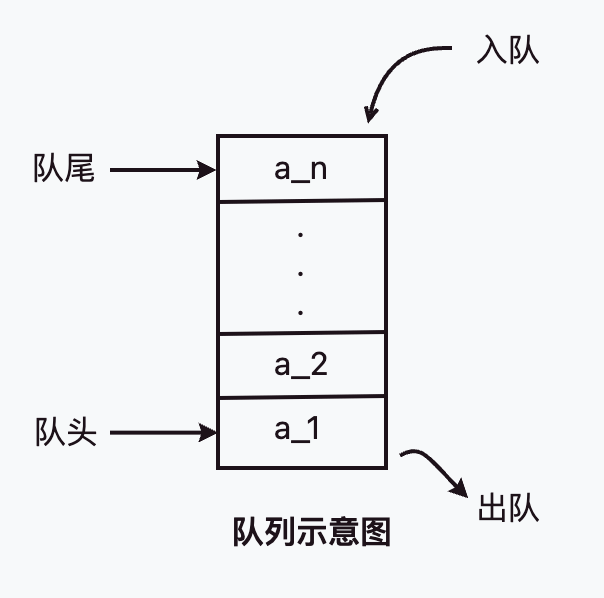
队列的基本运算有：

1. 置空队列
2. 判断队列空
3. 判断队列满
4. 入队
5. 出队
6. 取队头

队列定义

💡 C语言的看过来： 因为队列也是会存在上溢问题，如果将队列的存储空间定义得太大，则会产生空间浪费，因此可将数组空间想象为一个环形空间，称这种表示的队列为循环队列。 通过少用一个元素空间，在入队前，先判断尾指针在循环下加1后是否等于头指针，若相等则认为队列满。 下面C语言的实现也是主要介绍这种！

c

#define QueueSize 100
typedef struct
{
  DataType data[QueueSize];
  int front, rear;
} CirQueue;
CirQueue Q;

typescript

type SeqQueue = string[]
const QueueSize = 100
const seqQueue: SeqQueue = []

置空队列

c

void InitQueue(CirQueue *Q)
{
  Q->front = Q->rear = 0;
}

typescript

function InitQueue(q: SeqQueue) {
  q = []
}

判断队列空

c

int QueueEmpty(CirQueue *Q)
{
  return Q->rear == Q->front;
}

typescript

function QueueEmpty(q: SeqQueue) {
  return !q.length
}

判断队列满

c

int QueueFull(CirQueue *Q)
{
  return (Q->rear + 1) % QueueSize == Q->front;
}

typescript

function QueueFull(q: SeqQueue) {
  return q.length === QueueSize
}

入队

c

void EnQueue(CirQueue *Q, DataType x)
{
  if (QueueFull(Q))
  {
    printf("Queue overflow");
  }
  else
  {
    Q->data[Q->rear] = x;
    Q->rear = (Q->rear + 1) % QueueSize;
  }
}

typescript

function EnQueue(q: SeqQueue, x: string) {
  if(QueueFull(q)) {
    throw new Error('Queue overflow')
  } else {
    q.push(x)
  }
}

出队

c

DataType DeQueue(CirQueue *Q)
{
  DataType x;
  if (QueueEmpty(Q))
  {
    printf("Queue empty");
    exit(0);
  }
  else
  {
    x = Q->data[Q->front];
    Q->front = (Q->front + 1) % QueueSize;
    return x;
  }
}

typescript

function DeQueue(q: SeqQueue) {
  if(QueueEmpty(q)) {
    throw new Error('Queue empty')
  } else {
    return q.shift()
  }
}

取队头

c

DataType GetFront(CirQueue *Q)
{
  if (QueueEmpty(Q))
  {
    printf("Queue empty");
    exit(0);
  }
  else
  {
    return Q->data[Q->front];
  }
}

typescript

function GetFront(q: SeqQueue) {
  if(QueueEmpty(q)) {
    throw new Error('Queue empty')
  } else {
    return q[0]
  }
}

❗ 队列中除了比作循环队列，还有一种链式存储结构的队列，称为链队列，也能解决空间浪费问题，这里也不详细解析了，有兴趣可以自己实现一遍。

应用场景（列举部分）

1. 购票系统
2. 滑动窗口
3. 消息队列