K最近邻算法

在特征空间中，如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别，则该样本也属于这个类别。简单来说就是在特征的数据中，它附近大多数是啥，它就是啥。

KNN（K最近邻算法 ）两项基本工作：

1. 分类
2. 回归

分类

举例理解👇

比如有一个水果，它是未知的，只知道它的大小颜色，不知道橙子还是柚子？

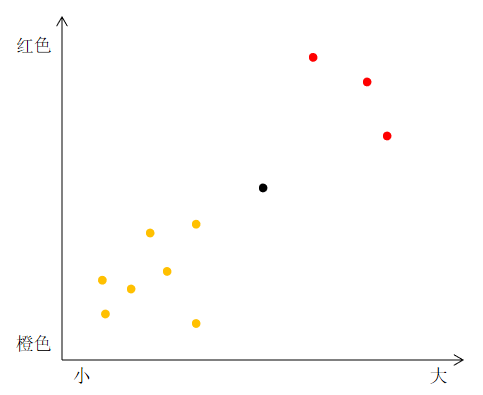
橙色点的为橙子🍊，红色点的为柚子🍅，黑点代表的是未知水果，他们的大小颜色分布如这个图表。

然后找几个它邻近的点，发现都为橙子的多，则我们就说这个水果（黑点）就是橙子。

这个思路就是K最近邻算法，图表就为特征空间。

思路分析🔍

首先特征抽取，你需要抽取一些用于比较的特征，比如这里比较的特征是大小和颜色。

	A	B	C
个头	2	2	4
红的程度	2	1	5

然后绘图略（类似上图）。最后一步计算使用毕达哥拉斯公式计算他们的距离👇

$$\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$

AB距离为1，AC距离为 根号13，BC距离为 2根号5。因此可以得知A和B很像。

举一反三，推荐系统也可以使用此算法计算。

回归

回归就是预测一个数字，根据它周围的相似情况，进行预测。

比如开发一个电影推荐系统，我们根据用户的电影各类型喜好情况绘图（类似上图），黑点为某一用户，我们需要为他推荐电影。

则我们可以推荐他周围邻近的用户（用户数自己定）喜欢的电影给他，因为他们是相似的（也可以使用毕达哥拉斯公式计算谁最相似则推谁的电影给此用户）。

如果他们都为电影A进行了评分，我们利用求他们评分的平均值来求预测该用户的评分，这就是回归。

如👇

相似用户	A	B	C
对同一电影评分	5	4.7	4.2

则预测黑点用户会评 4.6333分。

注意

邻近的点我们可以选择2个、3个，甚至100个都可以，因为此算法为K最近邻算法，并非二最近邻算法或三最近邻算法😂

简单来说，求出相似邻居的称为分类，可以是任意个。相似邻居的某个度量的求值预测称为回归。😶😶😶这是本人自己理解，有误请略过。

前面我们使用的是毕达哥拉斯公式计算他们的距离，但实际上使用更多的是余弦相似度。传送门已给，自己跳转了解。

注意

K最近邻算法 重点在于挑选合适的特征进行绘图。

没有万能的算法，必须考虑各种因素。

机器学习其实就是类似的原理，通过抽取一些特征，进行大量数据的训练。

当下一次的识别时，就会抽取特征进行相似对比，进而判断是什么。所有智能产品往往需要一个强大的数据库以及往后的机器学习。