LeeZhian Blog

Appearance

线性表 ​

为了方便理解概念，伪代码提供了 C语言 和 TypeScript。 使用 TypeScript 主要是为了对上 C语言的类型，方便理解。

线性表是由 n 个数据元素 a1, a2, …, an 组成的有序序列。

它的基本运算(仅列举常用的)有：

  1. 置空表
  2. 取表长
  3. 取表中第i个元素
  4. 按值查找
  5. 插入
  6. 删除

线性表的顺序存储 ​

将线性表的数据元素按其逻辑次序依次存入一组地址连续的单元里，称为顺序表。

⁉️ 疑惑点

根据概念，很容易想到的就是“数组”，它确实可以使用数组来现实顺序表，但不要弄混顺序表就是数组！

数据结构是对元素的描述，描述数据元素之间的逻辑关系。比如线性结构，树形结构等都属于逻辑结构。

而数组属于计算机中的物理结构（存储结构）。

假设线性表中的所有类型都是相同的，且每个元素需要占用 d 个存储单元，那么第 i 个元素 ai 的存储位置为 LOC(ai)=LOC(a1)+(i−1)∗d。

JavaScript是一门弱类型语言，它允许一个数组里存在多个不同类型的数据，但一般建议数组内所有数据类型一致。

c
#define ListSize 100
typedef int DataType;
typedef struct { // 定义一个顺序表结构体
	DataType data[ListSize];
	int length;
} SeqList;
typescript
// 在js中大多数使用数组来当成顺序表，毕竟 js 中并没有结构体这种语法
const seqList: Array<number> = [1, 2, 3]

➕ 插入算法

在线性表中，如果要在 i-1 与 i 之间插入一个新元素 x，那么

原线性表(长度为n)：(a1, a2, …, ai−1, ai, …, an)

新线性表(长度为n+1)：(a1, a2, …, ai−1, x, ai, …, an)

由此看出，只要插入的位置不是最后一个，则需要将原线性表的第i、i+1、…、n个元素分别后移一位。

注意：在某一些语言中，数组的长度在定义时已经确认，插入时需要注意地址越界问题；而在 js 数组属于动态数组，没有越界这一问题。

c
void InsertList(SeqList *L, int i, DataType x)
{
  int j;
  if (i < 1 || i > L->length + 1)
  {
    printf("插入位置出错");
    return;
  }
  if (L->length >= ListSize)
  {
    printf("越界");
    return;
  }
  for (j = L->Length - 1; j >= i; i--)
  {
    L->data[j + 1] = L->data[j]; // 向后一位
  }
  L->data[i - 1] = x;
  L->length++;
}
typescript
function insertList(seqList: number[], i: number, x: number){
	// js 中提供好了插入的方法，直接使用
	seqList.splice(i, 0, x)
}

最好情况下，时间复杂度为 O(1)；最差情况下，时间复杂度为 O(n)。

🗑️ 删除算法

原理与插入算法相反，若删除的不是最后一个元素，则需要将原线性表的第i、i+1、…、n个元素分别前移一位。

c
void DeleteList(SeqList *L, int i)
{
  int j;
  DataType x;
  if (i < 1 || i > L->length + 1)
  {
    printf("删除的位置出错");
    return;
  }
  x = L->data[i];
  for (j = i; j <= L->length; j++)
  {
    L->data[j - 1] = L->data[j]; // 向前一位
  }
  L->length--;
  return x;
}
typescript
function deleteList(seqList: number[], i: number){
	// js 中也提供好了删除的方法
	return seqList.splice(i, 1)
}

时间复杂度为 O(n)。

线性表的链式存储结构 ​

链式存储结构存储线性表数据元素可能是连续的，也可能不是连续的。因而链表的节点是不可以随机存储的。

💾 比如内存占用如下：

内存占用

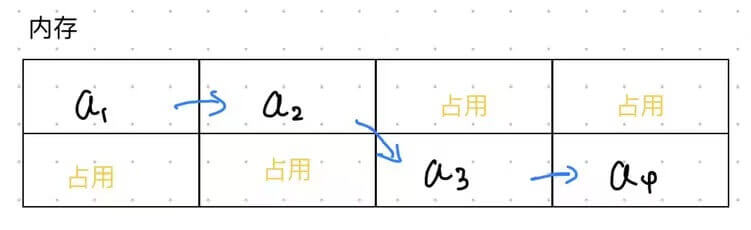
单链表 ​

每个结点包括两个域：存储数据元素的域称为数据域，存储直接后继存储地址的称为指针域。由于这种链表的每个结点中只包含一个指针域，因此成为单链表。

单结点结构👇🏻

单结点结构

链表结构👇🏻

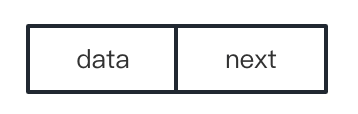
链表结构

head 为头指针，终端结点指针域为空，即为NULL。 如果链表中一个结点都没有，则为空链表，head=NULL。

🔵 结点定义

c
typedef struct node
{
  DataType data;     // 结点数据域
  struct node *next; // 结点指针域
} ListNode;
typedef ListNode *LinkList;
ListNode *p;
LinkList head; // 头指针
typescript
class ListNode {
	data: string | null
  next: ListNode | null
  constructor(data: string | null) {
	  this.data = data
    this.next = null
  }
}
  
class LinkList {
  head: ListNode
  constructor() {
    this.head = new ListNode(null)
  }
}

const linkList = new LinkList()

🖇️ 建立单链表

建立单链表常用方法有两种：头插法和尾插法。

这里主要介绍头插法，即将每次读入的新数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上。

尾插法其实差不多，只是新结点插入到链表的表尾上，自己可以尝试一下。

c
LinkList CreateList()
{
  LinkList head;
  ListNode *p;
  char ch;
  head = NULL;
  ch = getchar();
  while (ch != '\n')
  {
    p = (ListNode *)malloc(sizeof(ListNode)); // 申请分配一个类型为ListNode的结点地址空间
    p->data = ch; // 数据域赋值
    p->next = head; // 指针域赋值
    head = p; // 头指针指向新结点
    ch = getchar();
  }
  return head; // 返回头指针
}
typescript
class LinkList {
  // ...省略部分代码
  private _scanner() {
    return new Promise<string>(resolve => {
      const rl = readline.createInterface({ input, output })
      rl.question('请输入一段字符串（将会把每个字符设置为一个结点）', (answer) => {
        rl.close()
        resolve(answer)
      })
    })
  }

  async createList() {
    let head: ListNode | null = null
    const answer = await this._scanner()
    for (let i = 0; i < answer.length; i++) {
      const ch = answer.charAt(i)
      const listNode = new ListNode(ch)
      listNode.next = head
      head = listNode
    }

    if(head) {
      this.head = new ListNode(null)
      this.head.next = head // 头结点指向开始结点
    }
    
    return head
  }
}

🔍 查找

在单链表中，任何两个结点的存储位置之间没有固定的联系，每个结点的存储位置包含在其直接前趋的指针域中。

因此要查找一个数据，必须从表头节点开始搜索。

c
ListNode *GetNode(LinkList head, DataType k)
{
  ListNode *p = head->next;
  // 查找结点的数据值为k的节点
  while (p && p->data != k)
  {
    p = p->next; // 指向下一个节点
  }
  // 若查找成功返回查找结点的存储地址，否则返回 NULL
  return p;
}
typescript
class LinkList {
  // ...省略部分代码
  getNode(head: ListNode, k: string) {
    let p = head.next
    while(p && p.data !== k) {
      p = p.next
    }

    return p
  }
}

举例的是按结点值查找，还有一种按节点序号查找，课后题目，hh~

➕ 插入

根据链表的特性知道，每个结点都保存着直接后趋结点的存储地址。

因此我们很容易想到，（算法思想）如果要插入一个新结点到位置 i 上，那么需要找到第 i-1 个结点，然后将它的指针域改为指向新结点，新结点的指针域再指向会原来第 i 个结点，即可完成插入操作。

c
void InsertList(LinkList head, int i, DataType x)
{
  ListNode *p, *s;
  int j;
  p = head;
  j = 0;                         // 用于记录当前结点序号
  while (p != NULL && j < i - 1) // 使p指向第 i-1 个节点
  {
    p = p->next;
    ++j;
  }
  if (p == NULL) // 插入的位置出错了
  {
    printf("出错了");
    return;
  }

  s = (ListNode *)malloc(sizeof(ListNode));
  s->data = x;
  s->next = p->next; // p->next 是原来的第i个结点
  p->next = s;
}
typescript
class LinkList {
  // ...省略部分代码
  addNode(head: ListNode, i: number, data: string) {
    let p: ListNode | null = head
    let j = 0
    while(p != null && j < i - 1) {
      p = p.next
      ++j
    }
    if(p === null) {
      console.log('出错了')
      return
    }

    const newNode = new ListNode(data)
    newNode.next = p.next
    p.next = newNode
  }
}

时间复杂度为 O(n)。

插入新结点示意图

🗑️ 删除

删除算法的思想，其实和插入差不多，比如删除第 i 个节点，先找到第 i-1 个结点，然后使得 p→next 指向第 i+1 个结点，再将第 i 个结点释放掉即可。

c
// 删除第i个结点，并返回它的值
DataType DeleteList(LinkList head, int i)
{
  ListNode *p, *s;
  DataType x;
  int j;
  p = head;
  j = 0;
  while (p != NULL && j < i - 1) // 使p指向第 i-1 个节点
  {
    p = p->next;
    ++j;
  }
  if (p == NULL) // 删除的位置出错了
  {
    printf("出错了");
    return;
  }
  s = p->next;       // 第 i 个结点
  p->next = s->next; // 将 i-1 结点指向第 i+1 个结点
  x = s->data;       // 保存被删除第 i 个结点的值
  free(s);           // 释放空间
  return x;
}
typescript
class LinkList {
	// ...省略部分代码
  deleteNode(head: ListNode, i: number) {
    let p: ListNode | null = head
    let j = 0
    while(p != null && j < i - 1) {
      p = p.next
      ++j
    }
    if(p === null) {
      console.log('出错了')
      return
    }

    const s = p.next as ListNode
    p.next = s.next
    return s.data
  }
}

时间复杂度为 O(n)。

删除结点示意图

循环链表 ​

它的特点是单链表中最后一个节点（终端结点）的指针域不为空，而是指向链表的头结点，使整个链表构成一个环，这种形式的链表称为单循环链表。

它可以从任一个结点开始访问表中的其他结点。

基于它的特点得知，算法中循环的结束条件不再是 p 或 p→next 是否为空，而是它们是否等于头指针。

单循环链表示意图

双向链表 ​

在上面介绍的单链表和单循环链表的结点中只设有一个指向其直接后继的指针域；因此要访问某一个结点的直接前趋时，只能从头指针开始查找。

如果在单链表的结点中新增一个指向直接前趋的指针域，则形成两条不同方向的链，因此成为双向链表。

双向链表结点示意图

c
typedef struct dlnode {
	DataType data;
	struct dlnode *prev, *next;
} DLNode;
typedef DLNode * DLinkList;
DLinkList head;

双向链表存储结构示意图

双向链表的运算其实单链表没有多大的区别，只是要注意，插入和删除的时候，需要同时修改两个方向上的指针。

✔️✔️✔️ 双向循环链表同理。

🆚 顺序表和链表的比较 ​

顺序表链表
查询快慢
增删慢快
存储密度高较低（因为指针域占用了一部分）

存储密度=(结点数据域所占空间)/(整个结点所占空间)

Released under the MIT License.

Copyright © 2020-leezhian