狄克斯特拉算法

狄克斯特拉算法能够找出加权图中前往 X 的最短路径（这里并不一定是物理路径，也可能是某种度量指标最小的路径）。

注意：广度优先搜索，能够在非加权图中找出前往 X 的最短的路径，也可以理解为段数最少的路径。

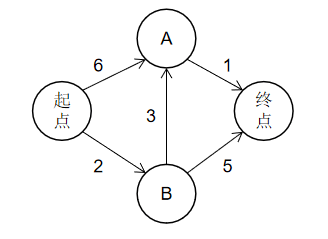
狄克斯特拉算法

上面那张称为加权图👆

如果是使用广度优先搜索，查找出来的起点到终点，最短是起点 → A → 终点。因为它只需两段就到达了。
如果是使用狄克斯特拉算法，查找出来的起点到终点，最快是起点 → B → A → 终点。因为他的权重最小，如果理解的话，可以把该例子的权重看成耗费时间。

加权图：带权重的图。即上图。

非加权图：不带权重的图。即上图把数值删掉。

环（边会形成一圈的图）👇

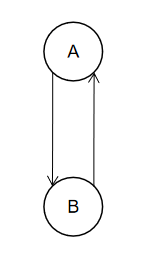
狄克斯特拉算法

无向图每一条边都是一个环，因为无向图两个节点彼此指向对方。狄克斯特拉算法只适用于有向无环图 。

TIP

图的算法，重点要学会怎么画图，画出图来分析就事半功倍。

注意

如果有负权边，就不能使用狄克斯特拉算法。在包含负权边的图中，要找出最短路径，可使用另一种算法——贝尔曼-福德算法。

什么是负权边？

比如你有一支笔，目标换一张MP4，现在可以一支笔直接换一张海报或加10块钱换一个收音机，海报换MP4要加60块钱，然后收音机换海报不但不用给钱，还可得15块钱。这就是负权边。

直接用笔换海报费用 0 元
先换收音机再换海报可赚 5元

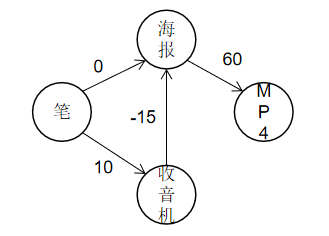
狄克斯特拉算法

实现👇（图一）

找出”最便宜“的节点，即某种度量最小的节点。即 B 节点。
更新该节点的邻居节点的开销。即 B 节点的所有邻居节点 A、终点。
重复这个过程，知道对图中每个节点都这样做了。
计算最终路径。

javascript

// 使用散列表表示 图
const graph = {
  start: {
    a: 6,
    b: 2
  },
  a: {
    fin: 1
  },
  b: {
    a: 3,
    fin: 5
  },
  fin: {}
}

// 实时保存节点开销
const costs = {
  a: 6,
  b: 2,
  fin: Infinity // 无穷大
}

// 保存节点父节点
const parents = {}

// 保存处理过的节点
const processed = []

/**
 * @description: 找出开销最低且未处理的节点
 * @param {object} costs 所有节点
 * @return {string} lowestCoseNode 开销最小的节点
 */
function findLowestCostNode(costs) {
  let lowestCost = Infinity // 最小开销
  let lowestCoseNode = null // 最小开销的节点

  // 遍历所有节点
  for (let node in costs) {
    const cost = costs[node] // 保存该节点的开销
    if (cost < lowestCost && !processed.includes(node)) {
      lowestCost = cost
      lowestCoseNode = node
    }
  }

  return lowestCoseNode
}

function lowest() {
  let node = findLowestCostNode(costs)

  while (node) {
    const cost = costs[node]
    const neighbors = graph[node]

    for (let key in neighbors) {
      const newCost = cost + neighbors[key]
      if (costs[key] > newCost) {
        costs[key] = newCost
        parents[key] = node
      }
    }

    processed.push(node)
    node = findLowestCostNode(costs)
  }
}

lowest()
console.log('最少开销是', costs['fin'])
console.log('路径是终点←', parents['fin'], '←', parents[parents['fin']], '←起点')
// 输出：
// 最少开销是 6
// 路径是终点← a ← b ←起点

至于这个怎么运行自己 debug 一下和自己画一下图就很清晰了。这题节点少好分析。

总结：

狄克斯特拉算法用于在加权图中查找最短路径。（注意这里最短路径的意思）
仅当权重为正时狄克斯特拉算法才有用。
狄克斯特拉算法只适用于有向无环图。

狄克斯特拉算法 ​

狄克斯特拉算法