贪心算法

贪心算法又称贪婪算法，概念是你每步都选择局部最优解，最终得到的就是全局最优解。

注意：贪婪算法并非在任何情况下都有效。

举例👇

背包问题，这是一个经典的问题。假设你是个贪婪的小偷，背着可装35磅重东西的背包，在商城伺机盗窃各种可装入背包的商品，你力图往背包中装入价值最高的商品。

假设你使用贪婪算法🤩🤩🤩：

盗窃可装入背包的最贵商品。
再盗窃还可装入背包的最贵商品，以此类推。

but 这次这种贪婪策略就不好使了。

比如你可盗窃的东西有以下

音响	笔记本电脑	吉他
$3000	$2000	$1500
30磅	20磅	15磅

分析👇

你背包可装35磅的东西，音响最贵，你把它给偷了，但背包再没有空间装其他东西。

这时你偷到的价值是3000美元。倘若你投的是笔记本电脑和吉他则总价值3500美元。

在这里，贪婪策略显然不能获得最优解，但非常接近。

提醒

有时候，你只需找到一个能够大致解决问题的算法，此时贪婪算法正好可派上用场，而且有时候最优解会付出的时间代价非常大，而贪婪相对会缩短大量时间且容易实现，和与正确结果相当接近。

思考
你要去欧洲旅行，总行程为7天。对于每个旅游胜地，你都给它分配一个价值——表示你有多想去那里看看，并估算出需要多长时间。你如何将这次旅行的价值最大化？请设计一种贪婪算法。使用这种算法能得到最优解吗？

举例👇

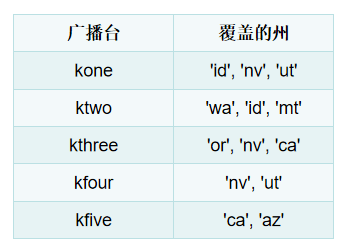
假设要办一个节目，要让全美所有州的听众都听得到；因而你需要决定哪些广播台播出，每个广播台都需要支付费用，你因此力图在尽可能少的广播台播出。

贪心算法

分析🤔

方案一：列出每个可能的广播台集合，然后筛选出覆盖全美的最小集合，如果广播台少尚且还可以，如果广播台很多的话，时间估计激增。

方案二：每次都选覆盖最多的，直到覆盖完毕。（即使用贪心算法，时间复杂度为O(n^2)）👇

javascript

// 需要覆盖的州
const needStates = new Set(['mt', 'wa', 'or', 'id', 'nv', 'ut', 'ca', 'az'])

// 每个电视台覆盖的州
const stations = {
  kone: new Set(['id', 'nv', 'ut']),
  ktwo: new Set(['wa', 'id', 'mt']),
  kthree: new Set(['or', 'nv', 'ca']),
  kfour: new Set(['nv', 'ut']),
  kfive: new Set(['ca', 'az'])
}

// 最终选择的电视台
const finalStations = new Set()

while(needStates.size) {
  let bestStation = null // 在某个条件下时最好的电视台
  let coveredStates = [] // 保存交集

  for(let key in stations) {
    // 求交集
    const covered = Array.from(stations[key]).filter(item => {
      return Array.from(needStates).includes(item)
    })
    // 是否覆盖的最多
    if(covered.length > coveredStates.length) {
      bestStation = key
      coveredStates = covered
    }
  }

  coveredStates.forEach(item => {
    needStates.delete(item)
  })

  finalStations.add(bestStation)
}

console.log(finalStations)
// 输出：
// Set { 'kone', 'ktwo', 'kthree', 'kfive' }

NP完全问题

比如上例就是NP完全问题，为解决集合覆盖问题，你必须计算每个可能的集合。

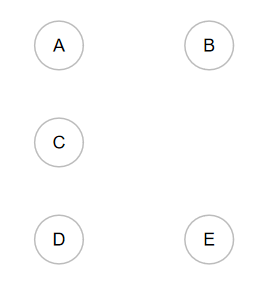
再比如旅行商需要前往5个不同的城市，他需要找出前往这5个城市的最短路径，为此，必须计算每条可能的路径。

贪心算法

分析🤔（基于起点不确定情况）

首先从简单开始，假如只涉及两个城市 A、B。有两条路线，A→B or B ← A。

为什么有两条，不是相同的吗？不一定，因为未必能原路返回，可能返回的路线需要绕一下。

假设再增加一个城市，路线有多少条？6条，自己画图就懂。

继续增加呢？24、120条等等

贪心算法

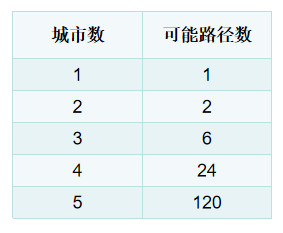
这被称为阶乘函数，随着城市数的增多，可能路线逐步暴增。这种问题都属于NP完全问题。

解决方案：使用近似求救，贪心算法。随机选择一个出发城市，然后每次选择下一个城市时，都选择还没去的最近的城市。

提示

NP完全问题的简单定义是，以难解著称的问题。

NP完全问题一般在元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。

比如在狄克斯特拉算法提到一个例子求最短路径，但如果加上一个要求，必须经过某几个点，则属于NP完全问题。

如果遇到属于NP完全问题，直接使用近似算法即可。

思考🤔
有个邮递员负责给20个家庭送信，需要找出经过这20个家庭的最短路径。请问这是一个NP完全问题吗？
在一堆人中找出最大的朋友圈（即其中任何两个人都相识）是NP完全问题吗？

贪心算法 ​

贪心算法