Knuth-Durstenfeld Shhuffle算法

Knuth-Durstenfeld Shhuffle 算法是洗牌算法（随机置乱算法）之一。

扩展

最早的洗牌算法 🔗 Fisher-Yates Shuffle算法

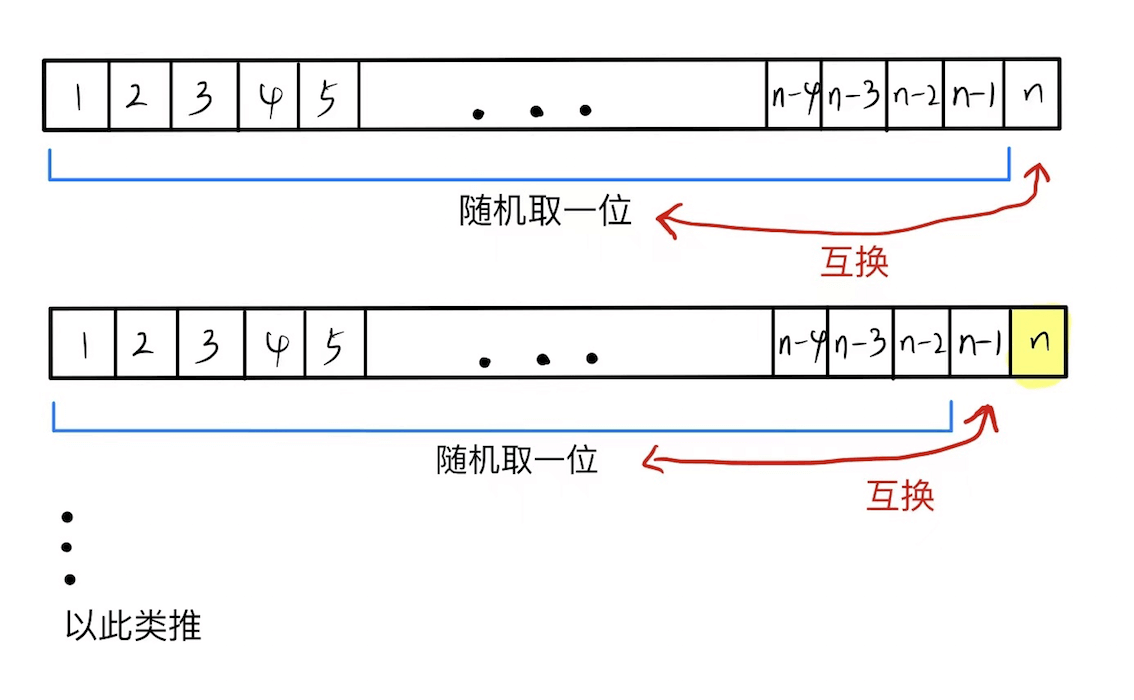
原理：每次从原数组中随机取一个元素，然后把该元素跟最后一个元素交换，即数组的尾部放的是已经处理过的元素。时间复杂度 O(n)，空间复杂度 O(1)。

特点：

随机性。
等概率，即每种结果的出现概率都应相同。

缺点：

必须知道数组的长度。

举例👇

假设有一副扑克牌 54张，现在要你把它洗乱，且每张牌都不能在原来的位置，要求是随机的。

如果没有 随机性 限制，大家可能很快都能想到一种方法：首尾置换，即第一个和最后一个置换，第二个和倒数第二个置换，以此类推，但如果加上随机呢？

算法步骤

建立一个数组大小为 n 的数组 arr。
生成一个从 0 ~ n-1 的随机数 x（因为待处理位置从 0 到该位置前中的数随机取一位，首次待处理位置为最后一位）
获取 arr[随机数] 的值，与待处理位置互换。
互换完毕后，待处理位置前移一位，重复步骤 2、3，直到所有位置处理完毕。

javascript

// 第一步
const poker = [
  1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22,
  23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41,
  42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54,
]

function shuffle() {
  let len = poker.length
  let temp;

  // 第四步
  while(len > 0) {
    // 第二步，Math.random() * len <=> (Math.random() * (len - 1 + 0 + 1)) + 0
    // 第一次范围为 [0, 53], 第二次[0, 52]
    const r = parseInt(Math.random() * len)
    len--
    // 第三步
    temp = poker[len]
    poker[len] = poker[r]
    poker[r] = temp
  }
}

shuffle()

Knuth-Durstenfeld Shhuffle算法 ​

Knuth-Durstenfeld Shhuffle算法