广度优先搜索

广度优先搜索又称为宽度优先搜索；是一种图的搜索算法。它是盲目的，它并不考虑结构的可能位置，而是展开检查图中所有节点，直到找到结果为止。通常使用队列的结构。时间复杂度O(人数 + 边数)

广度优先搜索解决的问题：是否存在A到B的路径，如果有，查询出来的路径是最短的。

图

图由节点和边组成，一个节点可能与多个节点直接相连，这些节点被称邻居。

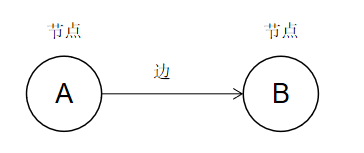
广度优先搜索

图还分为有向图和无向图。

有向图，边是有方向的，即上面例图。

入度：以某点为终点的边的条数，即 A 的入度为0，B 的入度为1。
出度：以某点为起点的边的条数，即 A 的出度为1，B 的出度为0。
度：入度 + 出度，即 A 的度为1，B 的度也为1。

无向图，边是无方向的，即例题中把边的箭头去掉，就变成无向图。

举例：你现在想要寻找一位可靠的代购，便宜代购一台笔记本，因此你在你朋友中查找👭🏻👭🏻👭🏻。

首先你会创建一个朋友名单，依次检查名单中每一个人，看看他是否是代购。如果是则完成，不是则继续往下检查。

假设你的朋友中没有代购，那么你就必须从朋友的朋友中查找（即加入到朋友名单中）。

这个过程就是广度优先搜索算法。

如图👇

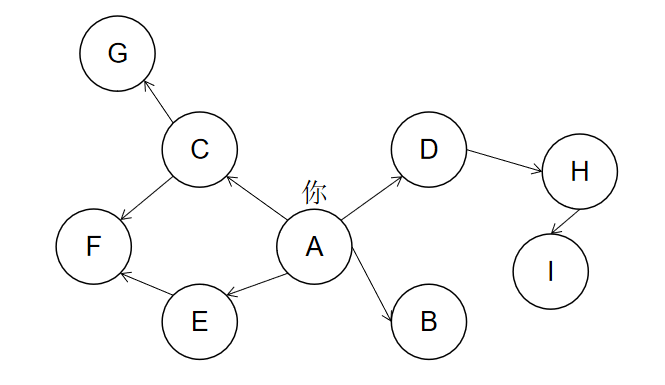
广度优先搜索

思考：
例图为有向图还是无向图？
A的出度、入度、度分别为多少？
F的出度、入度、度分别为多少？

分析图🧐

朋友是一度关系，即上图的 B C D E。

朋友的朋友是二度关系，即上图的 F G H。

以此类推，一度关系胜过二度关系，二度关系胜过三度关系...

实现这种目的的数据结构，最方便的就是队列。

什么是队列？

队列就是一种先进先出（First In First Out，FIFO）的数据结构，与栈（后进先出）不一样。打个比方，排队上公交车，排在前面的先上，后来添加的排在后面。从队列中取出一个元素称为出队，即上公交车的动作；将一个元素加入队列的称为入队，即去排队的动作。

代码实现

javascript

// 假设I为代购
// 判断是否是代购
function isAgent(people) {
  return people === 'I'
}

const friends = {
  A: ['B', 'C', 'D', 'E'],
  B: [],
  C: ['F', 'G'],
  D: ['H'],
  E: ['F'],
  F: [],
  G: [],
  H: ['I'],
  I: []
}

const find = (() => {
  let queue = friends['A'] // 初始队列
  const found = [] // 已查找

  return function () {
    while (queue.length) {
      const friend = queue.shift()
      // 判断是否已经查找过
      if (found.includes(friend)) {
        continue
      }

      if (isAgent(friend)) {
        console.log(friend, '是代购');
        return true
      } else {
        queue = queue.concat(friends[friend]) // 往后入队
        found.push(friend) // 记录已经查找
      }
    }
  }
})()

find()

解析：

首先将你的邻居添加到队列中
每次从队列中取一个出来，如果是代购则中止，如果不是代购则把他的朋友加入到队列中。
记录已经查找过的人。因为 F 分别是 C 和 E 的共同朋友，查找一次后没必要再做一次无用功。最重要的是避免 A → B → C → A 这种情况，如果不这样做，可能导致无限循环。

拓扑排序

有向无环图才有拓扑排序，即每一个顶点只出现一次，若 A → B，则不存在B → A。而且是有序的。

如：吃早餐 → 刷牙 → 起床，吃早餐依赖于刷牙，刷牙依赖于起床。

广度优先搜索 ​

广度优先搜索