动态规划

动态规划，它将问题分成小问题，并先着手解决这些小问题。

• 局部最优解👉贪心算法
• 全局最优解👉动态规划

使用场景：

• git diff实现
• 编辑距离等

说到动态规划，就不得不举例背包问题（贪心算法中提过），它是一个著名的例子。👇

给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

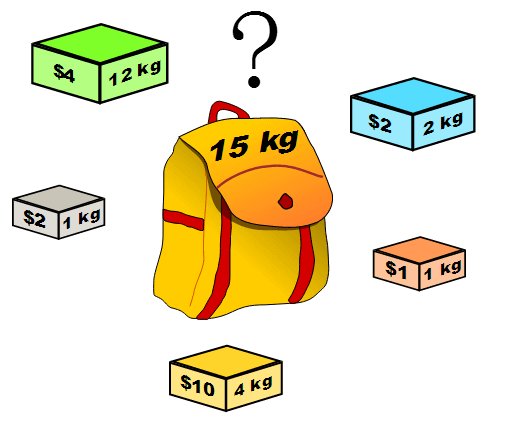
🎒背包问题案例分析

假设现在你有一个可装 4kg 的书包，力图往背包中装入价值最高的商品。有以下商品👇

音响	笔记本电脑	吉他
$3000	$2000	$1500
4kg	3kg	1kg

TIP

记住动态规划的要点，先解决子问题，再逐步解决大问题。

对于背包问题，先解决小背包（子背包）问题，再逐步解决原来的问题。

很多初学者一看到就直接开始算各种集合（当初我也是一样😂），然后自己坑了自己。

但数学老师往往会跟我们说，不要着急下笔，先分析问题，画图分析（因为图可以很直观的分析问题，表达问题的要点）。

这里也一样，**先画图分析（注意粒度的划分）**👇

每个动态规划算法都从一个网格开始，🎒背包问题的网格如下👇

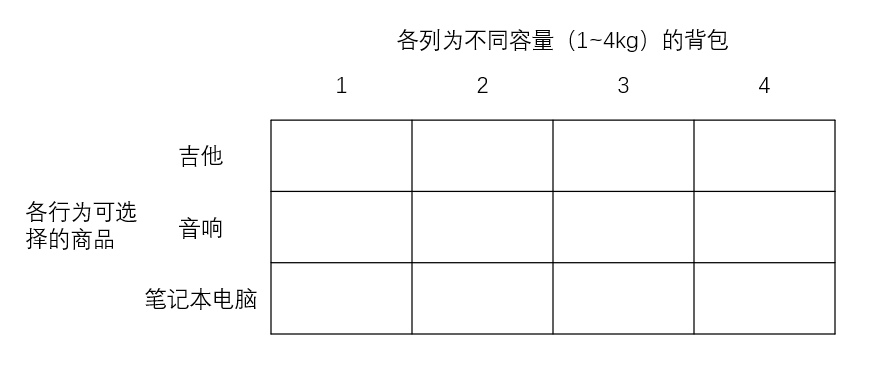
网格各行为商品，各列为不同容量（1~4kg）的背包，网格最初是为空的，当网格填满后就找到答案了。

首先第一行，吉他行🎸；吉他行，意味着你将尝试将吉他装入背包。在每个单元格，都需要做一个简单的决定：放不放吉他？

第一个单元格表示背包的容量为1kg。吉他的重量也是1kg，这意味着它能装入背包，因此价值为1500美元。👇

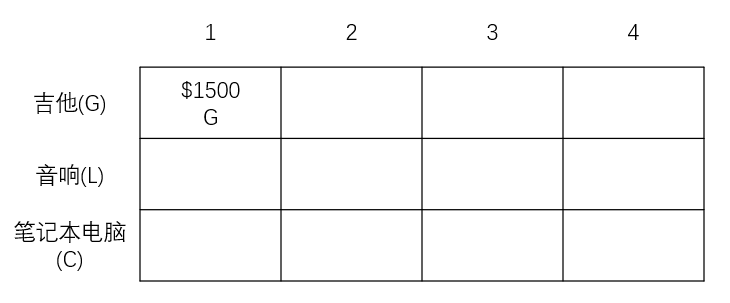
下一个单元格2kg，足够装下吉他。以此类推，这行的单元格都这样（因为这是第一行，只有吉他供你选择，你可以假设你现在只有吉他可以放）

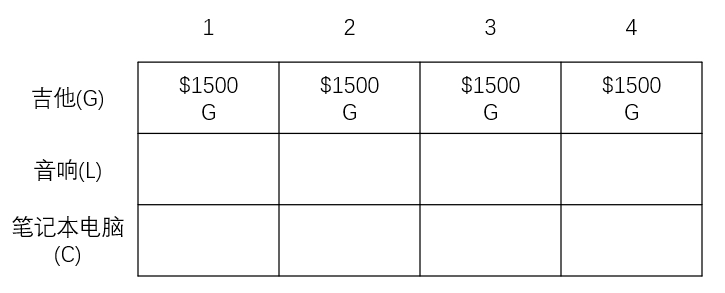
此时这行表示的就是背包的最大价值，如果背包为 4kg 的时候，商品的最大价值为 1500 美元。

为什么要分析 1kg 背包、2kg 背包，这明明是 4kg 背包呀？？？

因为动态规划先解决子问题，再逐步解决大问题

接着第二行，音响行🔊；这是因为是第二行，所以可以放的商品有吉他和音响了。在每一行，可放的商品都为当前行的商品以及之前各行的商品。

第一个单元格，1kg的背包。在此之前，可放的商品的最大价值为1500美元（放吉他），能不能音响呢？不能，音响太重了，1kg装不下音响，因此最大的价值依然为1500美元。👇

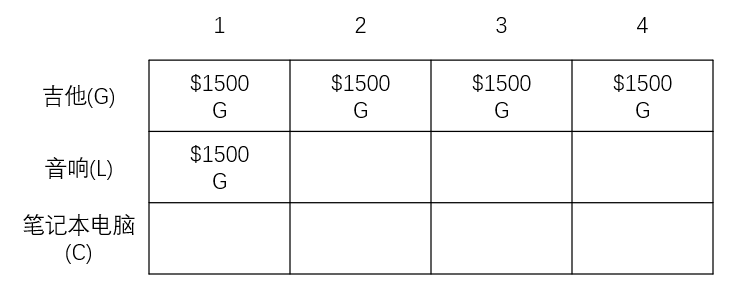
接下来第二、第三个单元格也一样，最大价值为1500美元，因为都是放不下音响。此时网格图如下👇

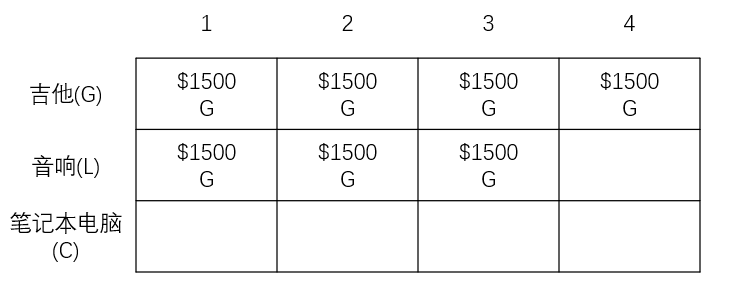
当背包容量为 4kg 时候，终于可以放下音响了。之前最大价值为1500美元，如果放音响而不是吉他的话，最大价值为3000美元，因此还是放音响。

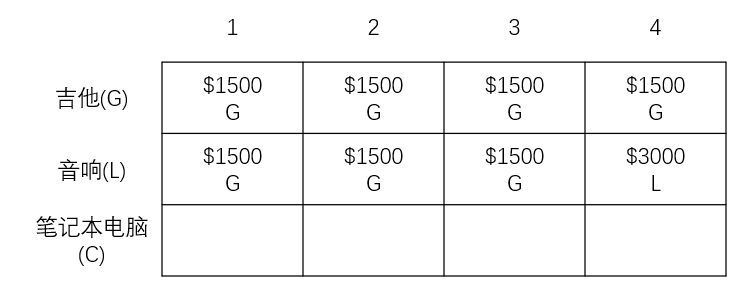
此时更新背包最大价值为3000美元。

第三行，笔记本电脑行💻。

在1kg 和 2kg背包时，没办法放笔记本，因此最大价值依旧为1500美元。👇

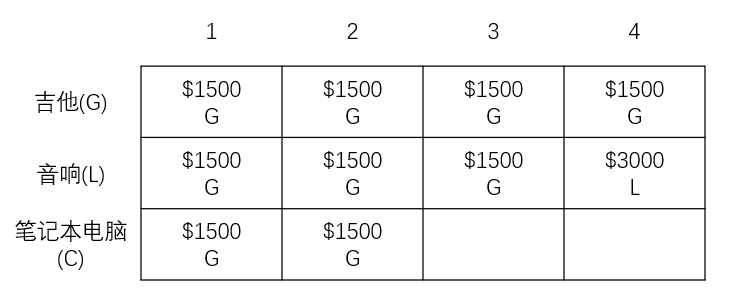
当 3kg 的时候，原来最大价值为1500美元，但现在有可供的笔记本电脑可放，因此更新最大价值为2000美元。

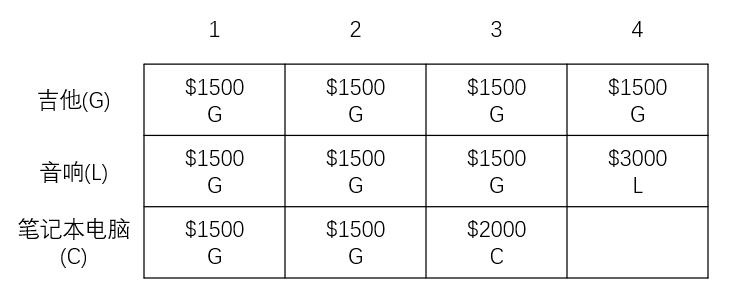
对于 4kg 背包的时候，当前最大价值为3000美元，但现在可以不放音响，放笔记本电脑，但它价值只为2000美元。🔍但它只有 3kg，还有 1kg 没有用到。然后查询 1kg 最大价值为多少？根据之前计算得知，在 1kg 的时候可以放入吉他，价值为1500美元。

因此，得出放入 笔记本+吉他（3500美元）大于放入音响（3000美元）。

这时候应该你会明白为什么要计算小背包问题了吧。因为在余下的空间时，则可以根据这些子问题来解决余下的空间可以放什么。即合并两个子问题来解决一个更大的问题。

最终网格图如下👇👇👇

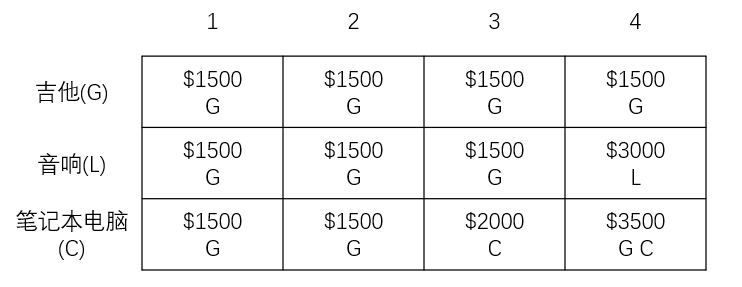
其实计算每一个单元格的时候都有一个公式📝（PS：此公式只在这问题上有效）

代码示例🙊

// 本代码只是一种实现方式，仅供参考。
const rucksack = 4 // 背包大小
// 商品信息; 也可使用多个数组来分别存储商品信息的重量和价值
const goods = {
  guitar: {
    weight: 1,
    price: 1500
  },
  loudspeakerBox: {
    weight: 4,
    price: 3000
  },
  computer: {
    weight: 3,
    price: 2000
  }
}

/**
 * @description: 求放入背包的最大价值
 * @param {object} goods 商品信息
 * @param {number} capacity 背包容量
 * @return {number} 最大价值
 */
function putIn(goods, capacity) {
  const grid = new Array(Object.keys(goods).length)
  for (let i = 0; i < grid.length; i++) {
    grid[i] = new Array(capacity + 1).fill(0)
  }

  let index = 0
  for (let key in goods) {
    const weight = goods[key].weight // 当前选择商品的重量
    const goodsPrice = goods[key].price // 当前选择商品的价值
    for (let i = 1; i <= capacity; i++) {
      const preRest = index - 1 < 0 ? 0 : grid[index - 1][i - weight]
      const price = i >= weight ? goodsPrice + preRest : 0 // 放入该商品时的最大价值
      const prePrice = index - 1 < 0 ? 0 : grid[index - 1][i] // 不放该商品时的最大价值，即上一个此容量是的最大价值

      grid[index][i] = Math.max(price, prePrice) // 返回两种情况中价值最大的那个
    }
    index += 1
  }

  return grid[index- 1][capacity] // 返回最大价值
}

console.log(putIn(goods, rucksack))
// 输出：3500

优化

1. 由于每行中的各列的最优解都需要考虑上一层节点的最优解，因此可以只保留两行。
2. 由于每次参考值都只需要取上一行和当前位置左边位置的值（因为剩余重量的最优解一定在左边），因此可以把问题转为从右向左求解，并且在求解的过程中不断覆盖当前列的值，而不会影响下一次求解。

如倒序遍历的，那么当发现它小于当前物品的重量时，说明不可能装下当前物品了，此时直接结束本层循环即可，因为左边的值一定是「不选当前物品时的最大价值」，也就是在上一轮循环中已经求得的值。

思考：如果再添加多一个商品呢？比如 2 kg 的手机，价值2000美元。

这里就不分析了，自己尝试画图分析。

WARNING

FAQ❓❓❓

1. 会不会沿着一列往下走时，最大价值有可能降低吗？

不可能。因为每次迭代时，存储的都为当前的最大价值，因此最大价值不可能比以前低。

2. 行的排列顺序会影响结果吗？

不会。你可以自己尝试一下。

3. 动态规划只能解决 ”拿和不拿“ 的问题，不能说只拿一半。如背包问题中，假设商品中添加一袋米，不能说背包还有空隙，则我把这包米打开，倒一点进去填满；只能说拿或不拿整袋。

4. 仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。比如规划在有限时间里去多个旅游景点，使评分最大，有故宫1.5天，评分9；长城1.5天，评分8；广州塔0.5，评分7等旅游景点。倘若你要去故宫和长城玩，按离散的是需要3天。但如果相互依赖的话，假设去北京只需要0.5天，到北京后去故宫和长城只需1天了，因此总时间为2.5天，这种改变会影响建模。

5. 动态规划得到的最终解时会出现两个以上的子背包（子问题）吗？

不会。动态规划的算法的设计，最多只需合并两个子背包，不会涉及两个以上的子背包，但允许子背包中可能又包含子背包。

6. 出现最优解的时候会出现没装满的情况吗？

会。比如商品有一个 3.5kg 的价值 100w 的钻石，4kg 的背包肯定拿它（价值比其他大得多），但剩余的 0.5kg 又放不下其他东西。

♾️ 最长回文子串 案例

Leetcode 第五题最长回文子串，其中一个解法：动态规划。

给你一个字符串 s，找到 s 中最长的回文子串。 输入：s = "babad" 输出："bab" 解释："aba"

🤔 分析问题：找出最长的回文子串，其实把它分解一下，假如我有一个回文子串，只要往两边加上同一个字符，那它还是回文子串。也就是说 bab 同时加上 c 得 cbabc。 所以只要从最小的子串开始，逐渐增大子串，判断首尾是否一样（首尾c），如果一样则判断包含的子串是否是回文（判断bab，在上一轮已经知道它的值），如果是则该子串也是回文。边界只要子串长度等于字符串长度则停止。

以 "babad" 案例网格图如下 👇🏻

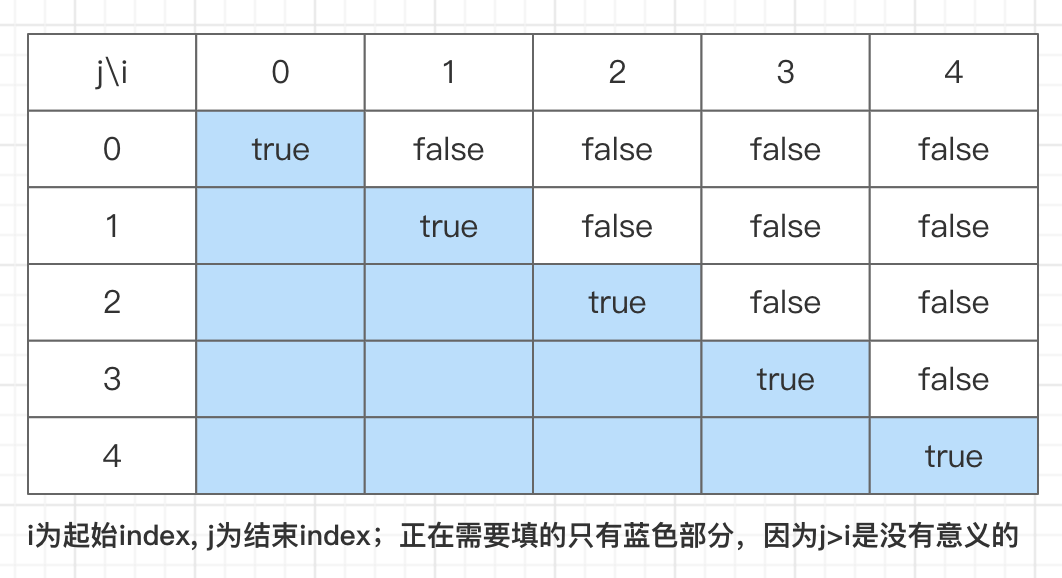
var longestPalindrome = function (s) {
  const len = s.length
  // 因为长度小于 2，肯定是它本身
  if(len < 2) {
    return s
  }

  let maxLength = 1
  let start = 0
  // 划分一个 len * len 的表格
  // i j 分别表示子串的起始index 和 结束index，因此 i = j 必定是true，即一个字母的时候
  // 同时注意 i > j 是没有必要或者说是不合法的，因此这个表起始也就只填一半（以 i = j 划出分界线）
  const dp = new Array(len)
  for (let i = 0; i < len; i++) {
    dp[i] = new Array(len).fill(false)
    dp[i][i] = true
  }

  const charArr = s.split('')
  // 以 案例 babad 举例
  // L 代表子串的长度，比如 L = 2时需要验证， ba(01)、ab(12)、ba(23)、ad(34)
  // L = 1时没有必要验证，因为肯定都为true，并且上面已经处理
  for (let L = 2; L <= len; L++) {
    // 搜索并检验 s 中所有长度为L的子串
    for (let i = 0; i < len; i++) {
      // j 的 坐标（子串结束坐标）
      const j = L + i - 1

      // 超出右边界
      if(j >= len) break

      // 判断首尾字符是否一样
      if(charArr[i] !== charArr[j]) {
        dp[i][j] = false
      } else {
        // 如果子串长度小于等于3，只要首尾一样则肯定是回文子串，比如 bab
        // 如果这里理解不了，可以修改为 L <= 3
        // 如果长度大于三并且首尾一样，则去掉首尾判断是否是回文，比如 cbabc，已知bab是回文，那么cbabc肯定也是回文，因为首尾一样（dp[i+1][j-1] 就是这个意思）
        if(j - i < 3) {
          dp[i][j] = true
        } else {
          dp[i][j] = dp[i+1][j-1]
        }
      }

      // 记录最长回文长度 和 起始index
      if(dp[i][j] && L > maxLength) {
        maxLength = L
        start = i
      }
    }
  }

  return s.substring(start, start + maxLength)
}

难点

动态规划可以帮助我们在给定约束条件下找到最优解。但难点不在于算法实现，在于如何设计动态规划解决方案。

1. 单元格的值是什么，即该使用什么样的公式？
2. 如何将这个问题划分为子问题？
3. 网格的坐标轴是什么？

这一点上，没有人能帮助到你，因为没有一个通用的计算公式来帮助你来计算单元格，只能靠自己经验或者大神解决过类似的方案得出。