快速排序

快速排序是一种排序算法，使用分而治之的策略，比选择排序快多了。同时它也是冒泡排序的一种改进，时间复杂度为O(nlog n)。

首先介绍分而治之是什么意思？

借用网上一个例子，假如一个农场主，有一块小土地，你要这块地均匀地分成方块，且分出的方块要尽可能大。

快速排序

步骤👇

找出基线条件，这种条件必须尽可能简单。
不断将问题分解，知道符合基线条件。

在这个问题中，基线条件就是一条边是另一条边的整数倍。

如一边长为30m，一条边为60m，那么最大的方块则是30m * 30m。

首先找出这块土地上可容纳的最大方块，得知是640m * 640m，即分成了三块（两块640m * 640m，1块400m * 640m）

快速排序

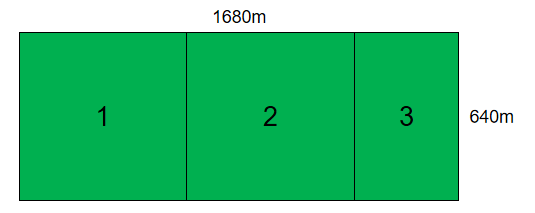
进而我们明白对余下那一小块可以使用相同的算法，因为适用于这小块地的最大方块，也是适用于整块地的最大方块。了解这个结论👉欧几里得算法

所以问题可以简化成均匀划分640m * 400m 土地的问题

省略的步骤

最大方块640m * 640m，余下640m * 400m
最大方块400m * 400m，余下400m * 240m
最大方块240m * 240m，余下240m * 160m
最大方块160m * 160m，余下160m * 80m

最后余下的这块土地满足基线条件，160是80的整数倍，因此对于最初的那片土地，适用的最大方块为80m * 80m。

快速排序

我们想一想，最简单的数组是怎么样的？

空数组
只包含一个元素的数组

因为在这种情况下，直接返回即可，不用排序，所以基线条件为数组为空或只包含一个元素。

分析❓❓❓

当包含两个元素的数组呢？

检查第一个元素是否比第二个元素小，如果小则交换位置即可。

当包含三个元素的数组呢？

使用分而治之，将数组分解，直到满足基线条件。首先选择一个元素作为基准值。

比如有数组 [60, 30, 10]，我们可以把数组第一个元素作为基准值60，然后找出比基准值小的元素以及比基准值大的元素。得到[30, 10] + 60 + [] 这三块，然后对于不满足基线条件的子数组重复第一步骤。

快速排序

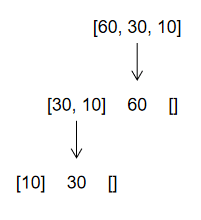
你会发现最终还是回到数组为空或只包含一个元素的情况。

代码实现🙊🙊🙊

使用递归的方法，每次返回都是排好序的左边 + 基准值 + 排好序的右边，则最终结果则实现了整体的排序。（什么时候排好序呢？数组为空或只包含一个元素）

流程图略。若不太了解，其实把这题画图分析一下，你会真相大白。

javascript

const arr = [2, 7, 9, 4, 5, 10, 1, 3, 6]

function quickSort(arr) {
  if (arr.length <= 1) return arr

  const temp = arr.shift()
  const less = arr.filter(item => item <= temp)
  const greater = arr.filter(item => item > temp)
  return [].concat(quickSort(less), [temp], quickSort(greater))
}

console.log(quickSort(arr))
// 输出: [1, 2, 3, 4, 5, 6, 7, 9, 10]

快速排序 ​

快速排序